How Galileo
Proved those
Spots were on the
Sun

Text Only

In an attempt to rescue the "perfectability of the heavens," which the Catholic
Church teachings required, Galileo's enemy Christoph Scheiner claimed
that sunspots were simply
undiscovered planets of the Sun occasionally
crossing in front of its disk. (Note that
Scheiner was inadvertently also acknowledging that the Sun could indeed
have planets, such as the Earth, encircling it).
Galileo responded to Scheiner by arguing that
sunspots change their shapes and that they are
often seen to originate on the solar disk and perish there.
Thus they could not be solar planets. They must reside on the Sun,
and therefore the Sun is not perfect.
But even these rational arguments did not silence Scheiner,
nor Galileo's other critics.
However, another of his arguments was so convincing that even Scheiner
eventually acknowledged the spots:

Galileo noticed that, while a spot took about 14 days to cross from one side of
the Sun to the other, its rate of motion was by no means uniform. That is,
the spot's motion always appeared much slower when near the edge of the Sun than
when near the center.
This Galileo recognized as an effect of foreshortening.
That is, a spot coming around the limb is
actually traveling towards you. But your eyes can't see the
3-D effect, and the spot likes as if it were moving slowing across
the disk. However, when the spot is in the middle 1/3 or so of
the Sun, all its motion is across the disk. So it appears to be
moving quickly.
Foreshortening would result if, and only if, the spot were on or very
near the surface of the Sun.
A planet orbiting the Sun would not appear to change its speed when
moving across the Sun's disk.
Let's describe this geometrically, as Galileo did:
Look at the figure, where the circle represents a view of the Sun
from above
and "you" represents you, an observer on Earth.
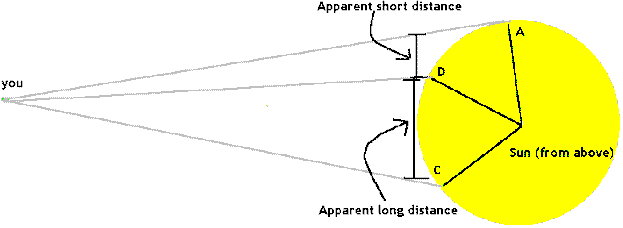
The points A, B, and C
are at equal distances apart on the surface of the Sun.
Assuming the Sun rotates at a constant rate,
the letters represent positions of a sunspot at equal intervals of time.
From your perspective, the spot moving from A to B only goes a little
ways, so appears to move slowly.
On the other hand, the spot moving from B to C covers a lot of ground, and
appears to move rapidly.
If the spot were a planet revolving some distance
away from the Sun, it's speed would not appear much different as the
planet went past the limb and then across the center of the Sun's image.
It requires only a simple calculation, performed
by Galileo, to express these results mathematically.
Can you prove Galileo's theory mathematically?

The only refutation of Galileo's conclusion was if there were indeed
planets revolving around the Sun, they were moving irregularly, and
always fastest when they crossed the center of the Sun's disk. No
sort of reason could be imagined for this behavior, and even if a reason
had been found, it would have again indicated that the mysterious planets
were moving out of harmony with the uniformity to which medieval astronomy
and the Church so strongly clung.


